Natural Forms & Spherical Thinkers

sus

sus

Moderator
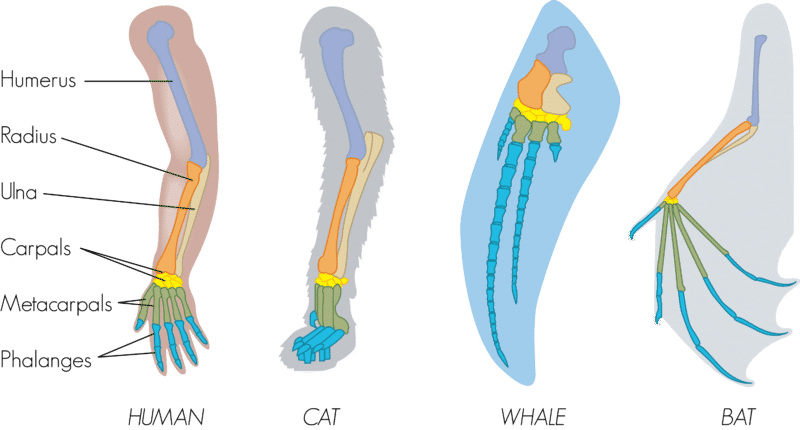
Tyler Volk is a biologist who wrote a book in the 90s called Metapatterns which I quite like. It works through these abstract forms—sheets, spheres, tubes, gradients, spirals, etc—across many, highly varied domains. Art, indigenous cosmology, astrology, biology. E.g. a sphere is volume-maximizing, relative to surface, so eggs and grapes and gravity-warped planets all end up approximating spheres. Sheets are the opposite, they're surface-maximizing, so they make for good interfaces between proximate systems. They make good pages of a book. Tubes also make good interfaces, but as paths of transport between distant systems: roads, wires, poles, channels. I'll post some excerpts in the (American) morning.

Anyway, he talks about "spherical thinkers" in his chapter on spheres. Spherical thinkers are well-rounded, they are developed in every direction. They bounce around a lot. I think he talks specifically about Buckminster Fuller, which is appropriate given the geodesic domes, but probably da Vinci is the most famous example.

I have a list that I'll post, of some of the great spherical thinkers, but perhaps others can add on.
 
sus

sus

Moderator
The other half of the title is "Natural Forms." It seems like spherical thinkers are always obsessed with geometry. It's all about finding formal and structural analogies/homologies across domains.

original_5e6e86838587d2a9b97c2cde45876c8f.png


Homologyexample-1.png
 
sus

sus

Moderator
OK my list right now, in chronological order, is:
da Vinci Spencer D'Arcy Thompson Joyce Huxley Fuller Bateson (@DLaurent) Brand & Volk

I'm sure there are many more important ones I'm missing
 
sus

sus

Moderator
One of the forms that I've been interested in for a while is the cell. I have a whole collection of images of cells. In addition to the obvious ones, like biological cells and prison cells.

The cell is a very simple and obvious pattern, it's basically just a series of bounded chambers, gridded modularity, tiling structures etc. Not revelatory or anything, but a simple place to start.

original_d4fcae21b83c1eeb5d42b024e8384cb2.png


Roman military town

original_0abd8e10e33d1e8d14a6f48d99af220e.jpg


Seripe Ghana city plan

original_f94259d2241ce3b57bfa9b1a2b997373.png


Garden plan

original_c2d401f2e0f4e83a903439d190111540.png


1833 Chicago town plan

original_332ed03f7514dd817b40086d06558850.png


Snakes at a local reptile expo

Matrix-pods.jpg


Matrix lifeharvesting pods
 
ghost

ghost

Well-known member
One of my favorite art books is called "Forms in Japan", and it just documents like, the pattern language of ways to attach things, combine things, make them extend eachother, etc. Big beautiful photos of examples of each. "Here's a pile of stones." And so on.

cbScreenshot 2024-12-02 at 02.18.43@2x.png
 
sus

sus

Moderator
Wagers that children make are formalized by hooking each other's little finger as a sign of their sincerity
 
Murphy

Murphy

cat malogen
sus said:
Wagers that children make are formalized by hooking each other's little finger as a sign of their sincerity
Click to expand...

pinky swears never caught on here, they’d be seen as one Americanism too far (but get what you mean)
 
version

version

Well-known member
sus said:
Anyway, he talks about "spherical thinkers" in his chapter on spheres. Spherical thinkers are well-rounded, they are developed in every direction. They bounce around a lot. I think he talks specifically about Buckminster Fuller, which is appropriate given the geodesic domes, but probably da Vinci is the most famous example.
Click to expand...

Does he offer examples of "sheet thinkers" too?
 
DLaurent

DLaurent

Well-known member
The name of the main Dutch historian I'm thinking of escapes me, he wrote a book on greek mythology when exiled from the nazis, but it was as epic as Huzinga or another Dutch theorist.
 
sus

sus

Moderator
versh said:
Does he offer examples of "sheet thinkers" too?
Click to expand...
No but that's very interesting. Tube thinkers too

Ostensibly a sheet thinker would provide a very broad interface between two fields. Or would create a very large surface to build upon. Perhaps someone like James, with Principles Of Psychology
 
You must log in or register to reply here.
Top